お断り
この記事で書かれている内容は,かなり特殊ななものです.通常の信頼区間を知らない人は読まないことを勧めます.
はじめに
このブログ記事では,Neyman流の信頼区間と,Fisher流の推測区間(fiducial interval)の違いを,次の2点に注目して解説していく.
その際,Fisherによる1930年論文 "Inverse Probability"をもとに,Fisherの考えを紹介していく.
なお,このブログ記事では,設定しているモデルが正しいものとして話を進める.<モデルの前提が正しい>ものとして議論を進めていくことに対する批判としては,Kass(2011) Statistcal Inference:The Big Picture, Statistical Science, 26(1), 1-9を参照のこと.
実現信頼区間の解釈における違い
信頼区間(推測区間)のうち実際に得られたデータ値を代入して得られた信頼区間(推測区間)を,ここでは実現信頼区間(実現推測区間)を呼ぶことにする.Neyman流信頼区間とFisher流推測区間の違いのひとつは,実現信頼区間(実現推測区間)の解釈にある.
実現信頼区間に対する解釈の両者の違いの根底には,<研究者や科学者が行う不確実性をもつ判定を,確率的に表現できるか? また,確率的に表現すべきか?>に対する哲学的な違いがあるだろう.Fisherは,少なくとも1930年では「できる」し「するべき」という立場であった.一方,Neymanはおそらく「できない」という立場であった.
Neymanが提示した例として,円周率の1000桁目は確率変数ではなく定数である,というものがある.「
=8である確率は?」と問いかけたならば,Neymanは0%か100%であると答えるであろう.一方,Fisherは,おそらく,「20%」などと確率的な言明をするのも有用だと考えていたと思われる.
<不確実な判定に対しても,積極的に確率的な言明をする>という1930年以降のFisherの立場は,Bayes流推測の基本方針に近い.Fisherの1930年論文のp.528第1段落を読むと,一瞬,Bayes推測をFisherは否定しているように読める(ただし,Bayesは擁護している).しかし,第2段落を読むと,Fisherが批判しているのは,Laplace流による事前分布の設定方法だけである.Fisherが批判しているのは,「不十分理由の原則」によって「同様に確からしい」として一様な事前分布を割り振っている点だけである.<不確実な判定に対して,積極的に確率的な言明をする>というBayes流の基本方針自体は,Fisherは批判していないどころか,1930年論文の主目的であり,「推測区間」によって技術的に達成しようとしている.
<不確実な判定に対して確率的な言明をする>よりも話題を狭くすると,<パラメータに対する確率的言明は行えるのか?」について,NeymanとFisherは異なった考えを持っていた.Neymanは,おそらく「行えない」と考えていたのに対して,Fisherは少なくとも1930年の段階では「行える」と考えた.
ただし,Fisherも1930年より前には,パラメータに対する確率的言明を(技術的に)行えるとは考えていなかった.確率分布をパラメータの関数とみなしたものを,「確率」に意味や用法は似ているけれど「確率」と区別する用語として,わざわざ「尤度」という言葉をFisherは割り振った.尤度は,確率がもつ性質は持たない.Jacksonさんの身長とJohnsonさんの身長から「JacksonさんもしくはJohnsonさんの身長」を一意に決めることはできないのと同様に,尤度も,たとえ排反なパラメータ値であっても,足し算を行えない.一方,確率は事象が排反であれば,足し算が行える(1930年論文,p.532).
尤度や最尤法を統計的推定の中心とみなしていた前期においては,Fisherはパラメータに対して確率的言明を行えるとは思っていなかった.1930年のこの論文では,その考えを変更している.この変更は,論文集にて<考え方を変えた>とFisher自身で述べている珍しい例である.Fisherは,いくつか重要な事項に対して考え方を途中で変更しているが,それを明示的に述べたことはあまりない.
以上のような出発点での違いから派生したのだと思われるが,例えば,「」というパラメータに対する確率に対して,NeymanとFisherでは次のような違いがあるだろう.
- Neymanの考え方では,
は,0%か100%のいずれか.
- 1930年以降のFisherの考え方では,
に対して,20%などの確率的言明が行える.
このような違いがあるために,実現信頼区間に対する解釈が両者で異なっていた.Neymanは,実現信頼区間にパラメータの真値が含まれている確率は0%か100%であると考えた.Fisherは,95%などの確率的言明が行えるとした.
現在の多くの統計学入門書では,Neyman流の立場のみを解説している.ただし,竹村彰通『現代数理統計学』の9章3節では,節の後半でわずかであるが,コイン投げをしてコインを覆っている場合を例に挙げて,Fisher流解釈を紹介している.
同一母集団からの抽出 vs 準拠集合からの抽出
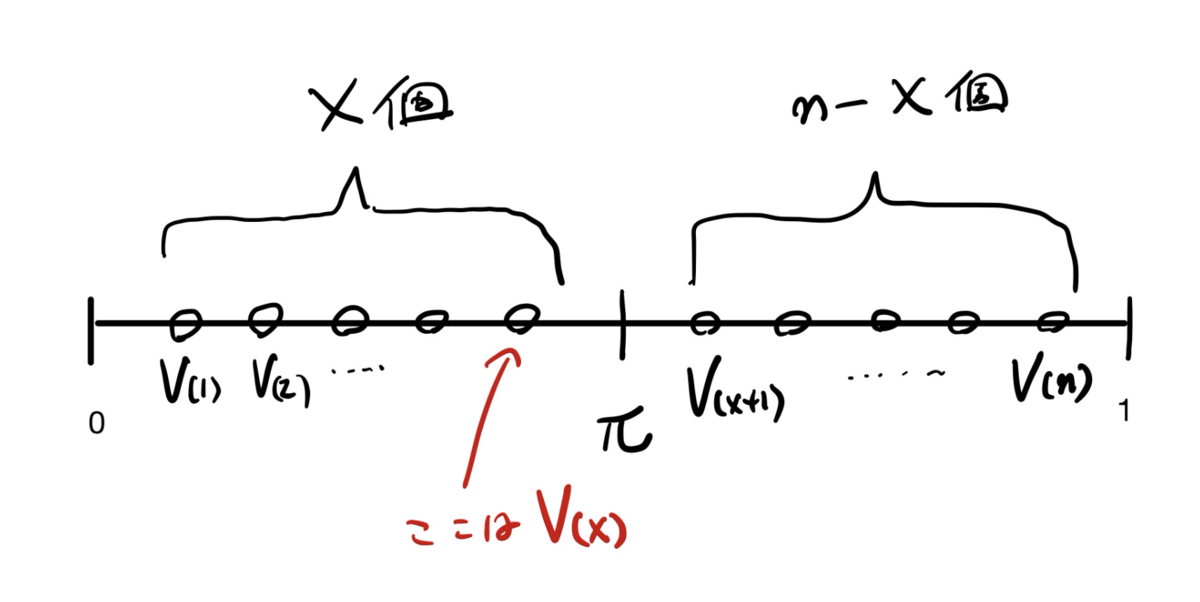
Neyman流信頼区間は,少なくとも教科書的な枠組みでは,同一母集団からの繰り返し抽出を前提としている.統計学の入門書では,例えば,95%信頼区間は,<同一母集団から100回繰り返し無作為抽出をした場合に,そのうちの約95%の区間内に真値が属する>などと説明される.これは,次の図1のようなイメージ図で描くことができよう.
Neyman流信頼区間の解釈では,前節で述べたように,1つ1つの実現信頼区間に真値が属する確率は0%か100%と考える.「95%」という確率は,あくまで100回や1000回などの同一母集団からの繰り返し抽出での確率である.この時,抽出元の母集団は同一であり,母集団分布のパラメータ値は1つの値に固定されているものと考える.
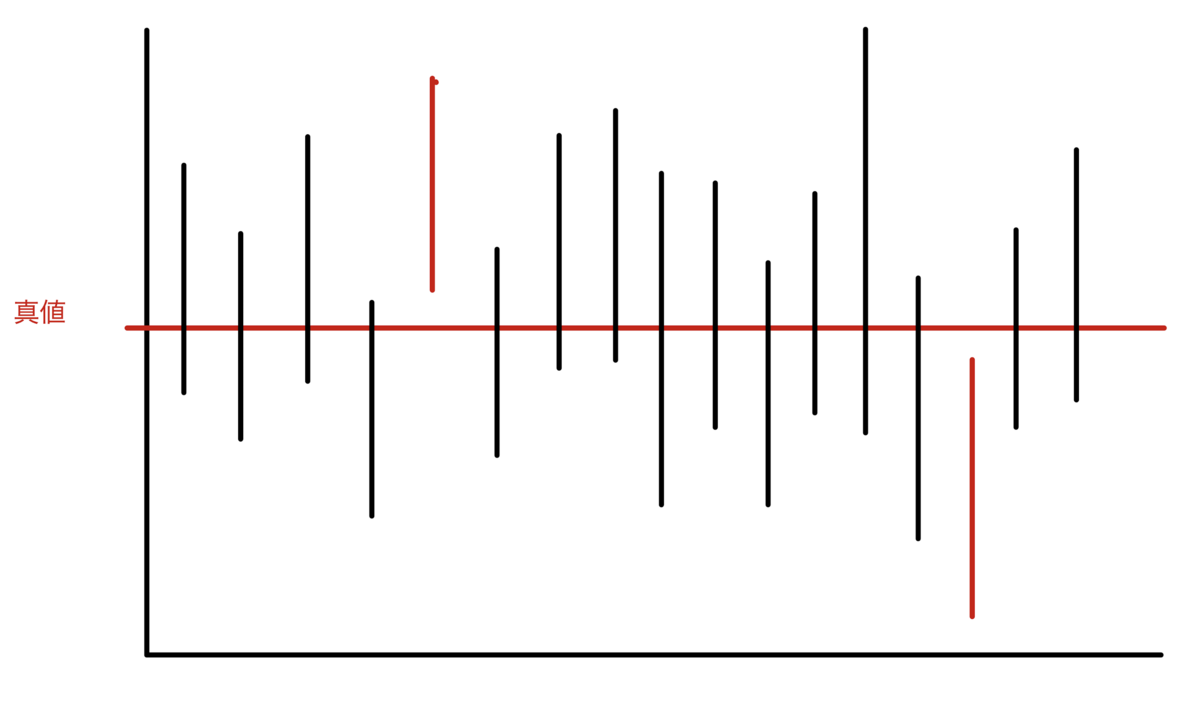
一方,1930年論文において,Fisherは,やはり抽出を考えているが,抽出元の集合は,同一の母集団でなく,いくつかの異なる母集団であっても構わないとした.Fisherの推測区間のイメージ図は,次の図2のようになる.

図2において,赤い点がパラメータの真値である.1930年論文では,図2のようにパラメータ値はばらついていても構わないと想定されている.つまり,Fisherの1930年論文で展開されている枠組みでは,パラメータは固定値ではなく確率変数であってもなくても構わない.
この設定のもとで,Fisherは,Bayes流推測とは違い,事前確率を設定せずに,<不確実な判定に対する確率的な表現>や<パラメータに対する確率的言明>を求めようとした.
図2において,私たちは,どの実現推測区間が真値を含んでいるかの区別がつかない.ただ,そのうちの95%は頻度的に真値を含んでいる.その場合,いま目の前にある実現推測区間に真値が属する確率は95%と思っていい ... というのがFisherの主なアイデアであろう.このアイデアをもとに,技術的には,パラメータ値を所与としたときの統計量の頻度的な確率分布を形式的に裏返すことで,パラメータ値に対する"確率分布"を求めた.この確率分布は,(少なくとも1930年の論文が設定しているような単純な前提ならば)少なくとも形式的には,確率の公理を満たしている.
この話だけを聞くと,Neyman流信頼区間とFisher流推測区間には,数値的にも大きな違いがあると思うかもしれない.しかし,1930年論文で扱っているような,連続型確率分布で,かつ,局外パラメータがないような単純な場合には,両者は数値的には同じである.1930年論文が扱っている単純な状況では,Fisher流推測区間は,技術的には,枢軸量(pivotal quantity)を用いて求めるのだが,それはNeyman流信頼区間を求める方法でもある.
Fisherは,1930年より前で最尤推定を推定の中心と考えていた時期には,同一母集団からの繰り返し抽出をもとに理論を整備していった.しかし,1930年以降になり,その考えを捨て,統計的推測での確率計算は,参照集団(reference set)に基づき行うべきものと主張するようになる.Fisher正確検定(Fisher直接確率検定)などにおいて,FisherとNeymanの哲学的な違いは目立つようになる.
注
以上の議論は,いずれの立場であっても,前提としているモデルが正しいものとして論じた.<モデルの前提が正しい>ものとして議論を進めていくことに対する批判としては,Kass(2011) Statistcal Inference:The Big Picture, Statistical Science, 26(1), 1-9を参照してほしい.