お断り
この記事はすぐに削除するかもしれません.
このブログ記事の目的
このブログ記事では,二項分布の確率に対する「正確」信頼区間が保守的になることを,二項分布の背後に一様分布を想定することで,直感的に分かりやすくなることを狙っています.
設定
以下のような,未知の事前分布と二項分布
の条件付き分布で構成される階層モデルを仮定します.
ここでは未知とします.
は,
のように定数であってもOKだとします.
となるいい感じの
や,
となるいい感じの
を求めたいとします.
ここで,や
は上記の不等式を満たしますが,「いい感じ」ではありません.
はなるべく大きく,
はなるべく小さくなるように努力するとします.
そのようなおよび
を求めれば,
となります.
という性質を持つ
は,
に対する信頼係数95%の信頼区間と呼ばれています(注:ただし,Neyman-Pearson流頻度主義の信頼区間では,固定された定数と
を仮定することがほとんどです.一方,中期R.A.Fisherの推測区間 fiducial limitでは,
は定数でも確率変数でもどちらでもいいとされています.いずれにしろ,
が定数であっても確率変数であっても以下の議論には影響しません.なお,R.A. Fisherの推測区間は,現在の教科書にはまず出てきません.)
なお,実用上では,に,
の実現値
を代入した
が報告されます.しかし,以下で問題としているのは,
と
です.
上と下で等しい確率(今回の場合は0.025)の信頼区間は,等裾信頼区間と呼ばれています.簡単のために,このブログ記事では,等裾信頼区間のみを考えます.
また,信頼区間には,データ以外のランダマイザー(確率発生装置)を用いるものもあります.そのような確率化された信頼区間もこのブログ記事では考えません.
背後に一様分布を想定
上記の信頼区間を求めるのに,独立同分布の一様分布に従う個の確率変数を背後に想定します.
このそのものは観測できず,
以下となっている
の個数
は観測できるとします.
が与えられた元で
以下となっている
の個数は,二項分布
に従います.
このような問題に置き換えると,元の問題は,のように
から
が決められるときに,
を満たす
や,
を満たす
を求めることに置き換えられます.
L(X)を求める
いま,の小さい方から,
番目の値を
と記すと,下図のような関係となっているため,
です.
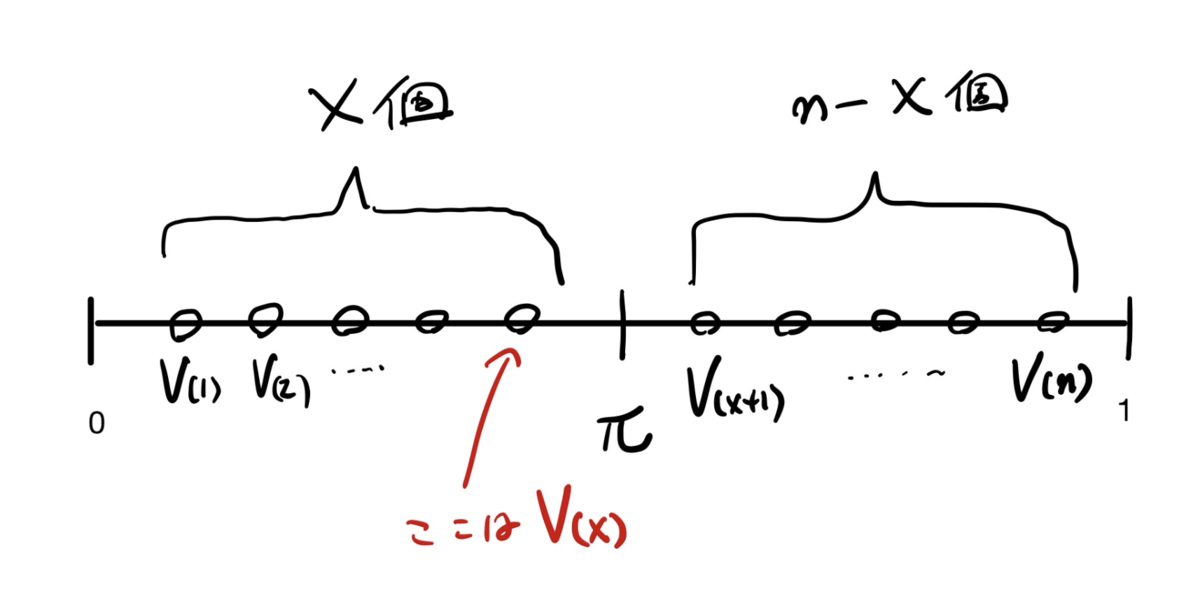
ですので,
となるように
を設定すれば,
は満たされます.
は,
が与えられれば,
に依存しません.よって,期待値を取るのを
に変えて,
を考えればよいです.
さらに,アダムの法則(Tower Property)から,
として,
を与えた時の
の分布を考えることにします.
独立同分布の個の一様乱数のX番目の順序統計量
は,よく知られているように,パラメータ
のベータ分布に従います.よって,
とすれば,
となり,
となります.
以上から,
となり,求めたい信頼区間の下限を求められました.
信頼係数が95%となる信頼区間は,ではなくて,
や
を使っても求まります.しかし,それは,
を使った時よりも小さくなります.
U(X)を求める
いま,の小さい方から,
番目の値を
と記すと,
です.
前節と同じように,しかし,今回はではなくて
について考えると,
とすると,
となります.
保守性はどこから来ているのか?
以上のように求められたは,等裾の「正確」信頼区間と呼ばれています.しかし,この信頼区間は次に述べる2点において,保守的になっています.
(注:頻度主義の用語において,下記の1番目は,「保守的」とは言われていません.通常,被覆確率が信頼水準よりも大きくなることだけを「保守的」と言います.)
第1に,この等裾「正確」信頼区間は,事前情報をまったく用いていません.そのため,もし事前分布が既知であり,その事前分布を用いて信頼区間(これは「信用区間」と呼ばれています)を求めた時よりも,信頼区間の幅は広くなるでしょう.
第2に,信頼区間の下限を求めるときにはよりも小さな値である
を用いています.また,信頼区間の上限を求めるときには
よりも大きな値である
を用いています.
や
の分布としては保守的ではない正確な分布を用いているのですが,それらは
よりも小さかったり大きかったりするので,そのため,そのズレだけ確率が0.025よりも小さくなります(つまり,被覆確率が信頼係数0.95よりも大きくなります).
このように考えると,「正確」信頼区間の保守性がどこから来ているのか,直感的に分かりやすいのではないかと思った次第です.
予測区間やFisher「正確」検定について
計算は複雑になりますが,ほぼ同様の枠組みで,二項分布の予測区間や,Fisher「正確」検定の保守性も理解できると思います.
もし興味がある方がいて,時間ができれば,その記事も書こうと思います.
お断り
この記事はすぐに削除するかもしれません.